引言
上一章讲解了遗传算法的基本思想与工作流程,构建了物种类Species及评价物种优劣的适应度函数。本章叙述如何利用求得的物种适应度去进行优胜劣汰的“选择算子”、物种间繁衍配对的“交叉算子”以及单个物种基因突变的“变异算子”。
选择算子
1 选择概率
物种\({s_i}(i = 1,2,…,n)\)的适应度\(f({s_i})\)已然得到,接下来就要利用\(f({s_i})\),求得它在整个种群中被选择(即遗传到下一代)的概率。这个概率表示为:\[p({s_i}) = \frac{{f({s_i})}}{{\sum\limits_{i = 1}^n {f({s_i})} }}\]产生了概率以后,我们便需要进行选择。
2 轮盘赌选择法
采用“轮盘赌选择法”,形象点说,就像我们经常见到的抽奖转转盘一样:
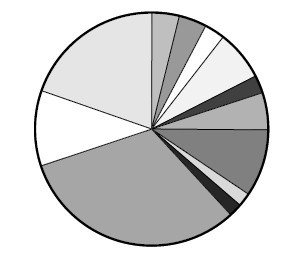
即每次筛选就相当于转动轮盘,概率大的面积就越大,自然就更容易被选上。那么“转”多少次呢?这里就涉及种群容量的约定了,我们如果选得过小,那么物种的多样性不够,很难有机会产生更优秀的物种(就像如果地球上其他生物都灭绝了,只剩人类,那么物种改变的机会,即路线更短的概率相对就越小了),而如果过大,那么算法的效率会降低,随机性更大,最后很不容易收敛。而根据一些文章和经验,每一轮我们就维持上一轮的种群容量大小即可,保持种群总量不变,即由初始种群的大小决定。那初始种群大小又选多大呢?这个参数就需要根据具体问题的规模来进行调整了,如果城市数很少,可以适当小一些,如果很多,就调大点。
3 选择过程
下面举一个实际例子来说明具体怎么选择。假设我们初始化了这样一个种群,也计算了他们的适应度、选择概率,得到如下的表:
| 物种编号 | 基因序列 | 路线长度 | 适应度 | 选择概率 | 轮赌命中次数 |
|---|---|---|---|---|---|
| 1 | 125367498 | 36 | 0.028 | 21.54% | 1 |
| 2 | 325974681 | 15 | 0.067 | 51.54% | 2 |
| 3 | 984723615 | 45 | 0.022 | 16.92% | 0 |
| 4 | 974613528 | 79 | 0.013 | 10.00% | 1 |
| 总和 | – | – | 0.13 | 100% | 4 |
从上表很容易看出:物种2因为路线较短所以适应度高,进而经过4次轮赌直接被选中了2次,而较次的物种1被选中了1次,物种3虽然适应度比物种4高,但由于算法的随机性并没有被选上,而是物种4“侥幸”被选上了。所以新的种群应该是这样的:一个物种1、两个物种2和一个物种4,即种群基因为:125367498、325974681、325974681和974613528。
4 精英保留策略
这里我们不难发现一个问题:倘若物种2的选中概率没有51.54%那么高,而是稍低一些(保证仍是种群中适应度最高的物种),那么这时它参与轮赌被选中的次数就难说有2次了,而很可能多多地让那些资质现在并非很好的物种1、3、4遗传到了下一代。但物种2仍是适应度最高的精英物种啊!让它怀才不遇,最后落得个沧海遗珠之憾,的确有失公平。
所以这时,我们加入一个“精英保留策略”,即并非所有物种均参与赌轮,而是在轮赌之前,先选出适应度最高的那个物种,复制若干个后提前进入下一代,接着再让剩余的物种参与赌轮进入下一代,最终两部分合成一个新种群。这样避免了因为概率原因,使得优秀物种沧海遗珠的情况发生,但这样做也容易陷入局部最优,所以多少个精英这个参数就需要不断地调整了,据一些研究经验来看,一般复制1/4效果是比较好的。
下面是整个选择算子的实现代码:
//选择优秀物种(轮盘赌)
void select(List<SpeciesNode> speciesList)
{
//计算选择概率
calRate(speciesList);
//找出最大适应度物种
float talentFitness=Float.MAX_VALUE;
SpeciesNode talentSpecies=null;
for(SpeciesNode species : speciesList)
{
if(species.fitness < talentFitness)
{
talentFitness = species.fitness;
talentSpecies = species;
}
}
//将最大适应度物种复制talentNum个
List<SpeciesNode> newSpeciesList=new ArrayList<SpeciesNode>();
int talentNum = (int)(speciesList.size() * tp); //tp:复制比重
for(int i=1;i<=talentNum;i++)
{
//复制物种至新表
SpeciesNode newSpecies=talentSpecies.clone();
newSpeciesList.add(newSpecies);
}
//轮盘赌speciesList.speciesNum-talentNum次
int roundNum=speciesList.size()-talentNum;
for(int i=1;i<=roundNum;i++)
{
//产生0-1的概率
float rate=(float)Math.random();
for(SpeciesNode species : speciesList)
{
if(species == talentSpecies || rate > species.rate) //精英物种或未选中,跳过
rate=rate-species.rate;
else //该物种在本次轮赌中选中
{
SpeciesNode newSpecies=species.clone();
newSpeciesList.add(newSpecies);
break;
}
}
}
speciesList = newSpeciesList;
}
交叉算子
交叉是对种群内两物种的基因序列进行裁剪组合的操作,一般以一定概率执行,而不是每次都执行。物种的配对选取最好随机,而不要1和2配对,3和4配对(因为在使用精英保留策略时很可能是连续追加进种群的,这样相当于近亲繁殖,很难擦出火花即产生路线长度比双亲都短的后代基因)。那么双亲的基因序列之间具体怎么交叉呢?
由于物种基因的编码形式是以“城市编号”为元素的,在实现交叉操作时首先任选一个位置作为起点,交换两个物种的后半段基因。但需注意的是,交叉后的后半段基因可能与物种的前半段基因重复,故而还需进行基因冲突处理,即把物种1所有重复的基因与物种2所有重复的基因对应交换。交叉操作具体如下图所示:
| 物种编号 | 基因序列 | 配对对象 | 交叉点位置 | 交叉结果(未去重) | 交叉结果(去重) |
|---|---|---|---|---|---|
| 1 | 125 | 367498 | 2 | 3 | 125 | 974681 | 325 | 974681 |
| 2 | 325 | 974681 | 1 | 3 | 325 | 367498 | 125 | 367498 |
| 3 | 97461 | 3528 | 4 | 5 | 97461 | 4681 | 97325 | 4681 |
| 4 | 32597 | 4681 | 3 | 5 | 32597 | 3528 | 46197 | 3528 |
具体实现代码如下:
//交叉操作
void crossover(List<SpeciesNode> speciesList)
{
for(int n=0;n<speciesList.size();n+=2) //两两配对
{
if(n+1 >= speciesList.size()) //已无可配对的母物种(种群容量为奇数)
break; //结束
SpeciesNode fatherSpecies = speciesList.get(n); //父物种
SpeciesNode motherSpecies = speciesList.get(n+1); //母物种
//交叉概率 pcl < rate < pch
float rate=(float)Math.random();
if(rate > Constant.pcl && rate < Constant.pch)
{
int crossPosition=rand.nextInt(Constant.CITY_NUM); //随机生成交叉点
List<Integer> fatherDuplicateGenesList = new ArrayList<Integer>(); // 存储父物种前半段所有重复基因的位置
List<Integer> motherDuplicateGenesList = new ArrayList<Integer>(); // 存储母物种前半段所有重复基因的位置
//后半段基因挨个位置进行互换
for(int i=crossPosition;i<Constant.CITY_NUM;i++)
{
//基因互换
int gene;
gene=fatherSpecies.genes[i];
fatherSpecies.genes[i]=motherSpecies.genes[i];
motherSpecies.genes[i]=gene;
//检测fatherSpecies.genes[i]是否与父物种前半段某位置基因重复,若是则记录
for(int j=0;j<crossPosition;j++)
if(fatherSpecies.genes[i] == fatherSpecies.genes[j])
fatherDuplicateGenesList.add(j);
//母物种同理
for(int j=0;j<crossPosition;j++)
if(motherSpecies.genes[i] == motherSpecies.genes[j])
motherDuplicateGenesList.add(j);
}
//去重
for(int k=0;k<fatherDuplicateGenesList.size();k++)
{
//父、母物种前半段重复的基因对应交换
int fatherGenePosition = fatherDuplicateGenesList.get(k);
int motherGenePosition = motherDuplicateGenesList.get(k);
int gene;
gene=fatherSpecies.genes[fatherGenePosition];
fatherSpecies.genes[fatherGenePosition]=motherSpecies.genes[motherGenePosition];
motherSpecies.genes[i]=gene;
}
}
}
}
变异算子
“变异”是跳出局部最优解的一个重要法宝,是对基因序列进行若干变换的一种操作,一般按非常小的概率执行。本文采用的是一种学界普遍认为效果较好的一种变异方式,即随机选取基因序列的两个位置k和m,逆转其k~m间的城市编号,即若现有物种:\[{s_i} = ({n_1},{n_2}, \cdots ,{n_k},{n_{k + 1}}, \cdots ,{n_{m – 1}},{n_m}, \cdots ,{n_n})\]随机产生1和n之间的两相异整数k和m,若k<m,执行逆转变换,得到新的基因序列:\[{s_j} = ({n_1},{n_2}, \cdots ,{n_m},{n_{m – 1}}, \cdots {n_{k + 1}},{n_k}, \cdots ,{n_n})\]
下面是代码:
//变异操作
void mutate(List<SpeciesNode> speciesList)
{
//每一物种均有变异的机会,以概率pm进行
for(SpeciesNode species : speciesList)
{
float rate=(float)Math.random();
if(rate < Constant.pm)
{
//寻找逆转的左右端点
Random rand=new Random();
int left=rand.nextInt(Constant.CITY_NUM);
int right=rand.nextInt(Constant.CITY_NUM);
if(left > right)
{
int tmp;
tmp=left;
left=right;
right=tmp;
}
//逆转left-right下标元素
while(left < right)
{
int tmp;
tmp=species.genes[left];
species.genes[left]=species.genes[right];
species.genes[right]=tmp;
left++;
right--;
}
}
}
}
结语
啊~累死了,遗传算法求解TSP的基本思想差不多就是这些啦。下一章将给出GeneticAlgorithm类的一个总控调用流程、遗传算法的一些常量参数定义及算法的实际运行效果。