引言
遗传算法通过借鉴大自然物种的进化规律取得了难以想象的效果,同样地,马上要介绍的蚁群算法也通过效仿蚂蚁嗅取信息素寻找食物最短路径的现象,取得了不相上下的效果,甚至在某些方面更优的效果。一些研究表明,蚁群算法有更强的健壮性和内在的分布并行性,非常容易与其他方法相结合,去解决比如网格任务调度、聚类分析、物流配送等问题。本文我们就简单地认识一下朴素的蚁群算法的设计思路与实现方案。
算法背景
蚁群算法,最早是1992年由Marco Dorigo在他的博士论文中提出的,是一种通过模拟自然界蚂蚁寻径的行为,提出的一种全新的模拟进化算法。据昆虫学家的观察和研究发现,生物世界中的蚂蚁有能力在没有任何可见提示下找到从其巢穴到食物源的最短路径,并能随环境的变化而变化,适应性地搜索新的路径,产生新的选择。这是因为蚂蚁在寻找路径时会在路径上释放一种特殊的分泌物——信息素,使得一定范围内的其他蚂蚁能够觉察并影响它们以后的寻径行为。当一些路径上通过的蚂蚁越来越多时,该路径上的信息素浓度就越大,后来的蚂蚁选择该路径的可能性就越大,从而进一步增加了该路径上的信息素浓度,这种选择过程称为蚂蚁的自催化行为(摘自一篇期刊论文)。就像下面这张图一样:
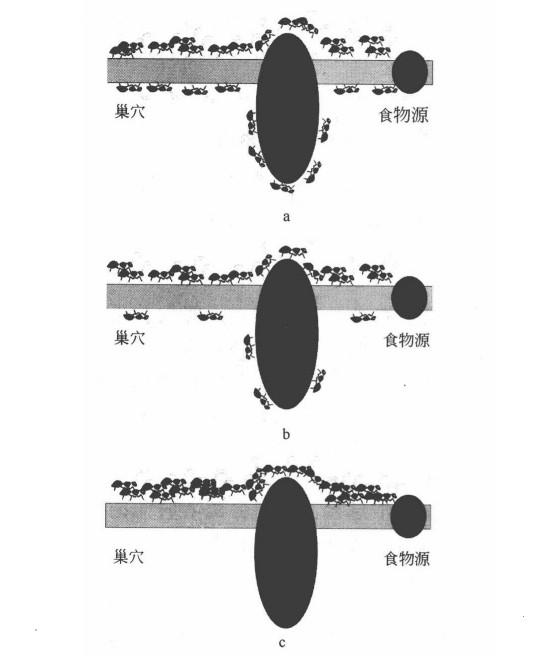
算法流程
相信到这里您还是一头雾水,是的,当初我也读过很多蚁群算法的文章,前面基本都是这样介绍的。直到后来逐字逐句阅读了算法流程和公式,再用代码实现以后才明白原来并没有那么困难。嗯,那下面我们马上说一下算法流程大概是什么样的,好有个宏观的感受。
Step1 初始化
将m只蚂蚁随机放置于若干城市上,让这m只蚂蚁逐个执行Step2的操作。
Step2 蚂蚁选路环游
若蚂蚁环游次数已满,转Step5;反之,设第k只蚂蚁当前正处在i城市,按照轮赌选择法选定下一步要到达的城市j。而蚂蚁k从城市i选择走城市j的概率\(p_{ij}^k\)是由如下公式算出的:\[p_{ij}^k = \frac{{{\tau _{ij}}^\alpha {\eta _{ij}}^\beta }}{{\sum\limits_{j \in \Lambda }^{} {{\tau _{ij}}^\alpha {\eta _{ij}}^\beta } }}\]
其中的参数意义如下:
m:蚂蚁总数
k:当前正在环游的蚂蚁(1<=k<=m)
i:蚂蚁k当前所处的城市编号
j:与城市i相邻可达的城市编号
\({{\tau _{ij}}}\):道路ij上信息素量大小
\({{\eta _{ij}}}\):道路ij的能见度大小,由\({\eta _{ij}} = \frac{1}{{{d_{ij}}}}\)得到,可以看到,道路ij长度越短能见度越高,越容易被蚂蚁选上
\(\Lambda \):与i相邻可达的所有城市j的集合
\(\alpha \)、\(\beta \):控制因子,\({{\tau _{ij}}}\)、\({{\eta _{ij}}}\)的次方数,调参用而已
一直选下去,直到环游完所有城市回到初始城市,记录下这条环游路径及其长度。
此时若所有m只蚂蚁均选好了下一个要找的城市j了,转Step3;反之转Step2,继续第k+1只蚂蚁的环游。
Step3 找最短环游路径
找出本轮这m只蚂蚁的最短环游路径及其长度\({{L_k}}\),记录之。
Step4 更新信息素
m只蚂蚁在本轮环游过程中已然在所经道路上留下的信息素,为量化他们在所经道路上留下的信息素,我们采用下面这个公式进行更新:\[{\tau _{ij}}(n + 1) = \rho \times {\tau _{ij}}(n) + \sum\limits_{k = 1}^m \Delta \tau _{ij}^k\]其中的参数意义如下:
n:m只蚂蚁环游的总轮数
\({\tau _{ij}}(n)\):前轮环游后,ij道路上的信息素总量
\({\tau _{ij}}(n + 1)\):本轮环游后,ij道路上的信息素总量
\({\Delta \tau _{ij}^k}\):本轮环游后,蚂蚁k在ij道路上产生的信息素增量
\(\rho \):挥发速率(0<\(\rho \)<1)
上式中还缺少\({\Delta \tau _{ij}^k}\)的求法,下面就给出它的计算公式:
\[\Delta \tau _{ij}^k = \frac{Q}{{{L_k}}}\]
其中的参数意义如下:
\({{L_k}}\):蚂蚁k该轮环游路线总长度
\(Q\):控制参数,用于调整信息素增量到适度范围
当按上述公式更新完每条道路的信息素后,便转Step2进行下一轮m只蚂蚁的环游。
Step5 输出最短环游路径
结语
以上便是蚁群算法的全部流程啦,关于流程图这里就不给出了,个人觉得上面已经描述得很清楚啦。本文参考了如下这篇文章ACO蚁群算法解决TSP旅行商问题的一部分(在此对作者表示感谢),大家也可以进行一些相关性阅读。下一章会给出对各部分的具体代码实现。